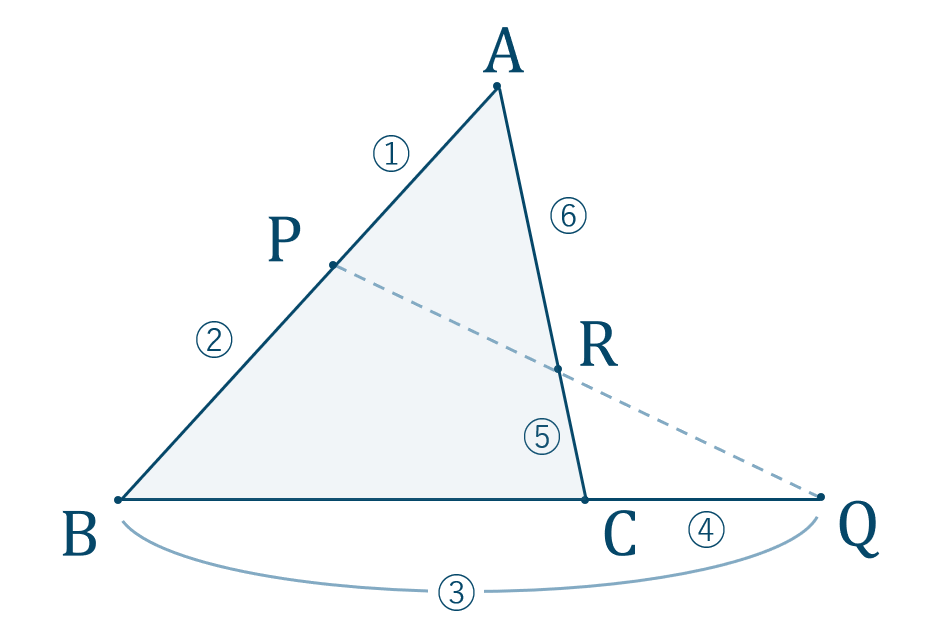
チェバの定理の構図だが,\ 3辺\mathRM{AB,\ BC,\ CA}のうち2辺の線分比が不明なので適用する意味がない \\2zh そこで,\ メネラウスの定理が適用できる三角形と1直線を探す \\2zh 与えられている線分比は\mathRM{ARRB,\ COOR,\ 求める線分比は\ CQQA}である \\2zh よって,\ \bm{\triangle\mathRM{ACR}を直線\mathRMこの証明は「相似条件とは?三角形の相似条件はなぜ3つなの?証明問題アリ」の記事でも詳しく解説しております。 スポンサーリンク 平行四辺形を作る 言い忘れてましたが、三角形と比の定理も 全く同じ方法 で証明ができます。 これが、冒頭で「この $2$ つの定理を区別する必要はすると ACDが30°60°90°の直角三角形になるので 辺の比を使ってAD,CDの長さを出す。 8AD=2 3 2AD=8 3 AD=4 3 8CD=21 2CD=8 CD=4 ≫ ABDは直角三角形なので、三平方の定理を使って x 2 =(4 3) 2 11 2 x 2 = x 2 =169 x=±13 x>0よりx=13 類題練習 ≫

15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext
三角形の比の定理
三角形の比の定理-(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。



中学数学 図形の相似
ケプラー三角形は三辺の比が等比数列となっている直角三角形で、その公比は黄金比 の平方根 であるような三角形のことである。 つまりケプラー三角形の辺の比は 、おおよそ1 :1272 :1618 である。 したがって三角形の一辺を辺とした正方形も黄金比を公比とした等比数列になる。検索語:三角比 三角関数の加法定理 三角比の三角形への応用 オイラー線の傾き 1 はじめに 高校数学「数学i」において三角比および三 角形などへの応用について学習する。応用の内 容は大体,正弦定理,余弦定理,三角形の解法, Point:三角形の垂心 定理三角形の3つの頂点から対辺に下ろした垂線は1点で交わる。 このとき、 交点 \({\rm H}\) を三角形の垂心 といいます。 また、垂線を3本引くので \(\triangle {\rm ABC}\) の内部で複数の直角三角形 ができます。
三角比の公式を使うためには直角三角形が必要でした。 直角三角形の 三平方の定理 もあわせて復習しておきましょう! 三平方の定理は 「c 2 =a 2 b 2 」 すなわち、 斜辺の2乗=底辺の2乗高さの2乗 で求まりましたね!②余弦定理をどこに当てはめるかを考える ( oab に適用する) 2辺と挟まれる角をどこにおいたらよいかが余弦定理を使う場合の問題点であるが、この場合 I 1 、 I 2 、 I 3 で囲まれている oab に着眼してほしい。 角度は 180°―θ を使うことに注意し、三角比の簡素化を図ると式がまとまりやすく このページでは、三角比・三角関数の公式をまとめています。 正弦・余弦・加法定理など 2つの視点から分かる公式の覚え方・考え方 三角形 \(abc\) に対して、点 \(a,b,c\) の内角をそ
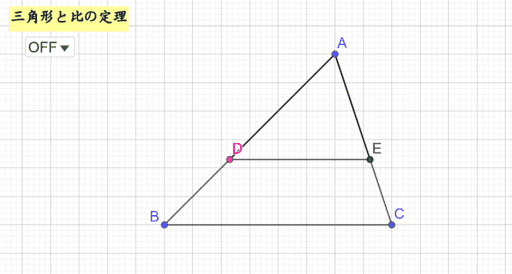
三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。 ルールは 2つの図形のパターン について 角を 内分 する「内角の二等分線」と、 外分 する「外角の二等分線」の 種類があります。 内角でも外角でも、 辺の比 は同じ関係式で表されます( 角の二等分線の定理 )。 まとめ:直角三角形の比3つを使い倒せ! 中学数学でよく使う直角三角形の比は次の3つ。 30、60の直角三角形 45の直角三角形 3 4 5の直角三角形 これを覚えるだけで三平方の定理を使わなくてよくなるから、 だいぶラクになるね。 いきなり覚えるのは
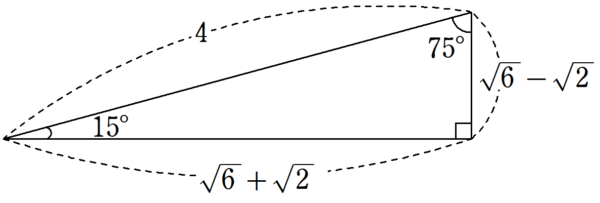



15 の三角比 Fukusukeの数学めも



三角形の角の二等分線定理 外角
それぞれ、底辺比に置き換えると、 (AF/BF)(BD/CD)(CE/AE)=1 となり、チェバの定理(拡張形)が証明された。 証明2(点Gが三角形の内角の対頂角の範囲内にあるとき) 辺の比を、三角形の面積比で表すと、 AF/BF= ACG/ BCG 三角形の面積比にまつわる公式たち 定理:三角形 a b c abc a bc の内接円と辺 b c bc bc の接点を d d d とおく。 d d d から辺 b c bc bc と垂直な直線と内接円の交点を e e e とおく。さらに a e ae a e と b c bc bc の交点を f f f とおくとき, b d = c f bd=cf b d = cf \( \frac{三角形ACX}{三角形BCX} = \frac{AF}{BF} = \frac{3}{2} \) ・・・(式2) 問題に辺の比が与えられているので、それを代入しておいたわけじゃ この式を、式2、と名前をつけておくかのぉ さらに、別の面積比を考えてみるかのぉ




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ
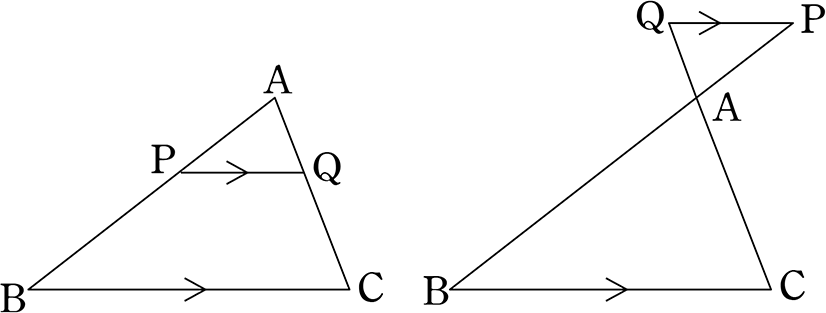
これは ade∽ abcで、それぞれの対応する辺の比が等しくなるためです。 ちなみに2つの三角形が相似になるのは、平行線の同位角が等しいことから、∠ade=∠abc、∠aed=∠acbとなり、相似条件の「2組の角がそれぞれ等しい」を満たすためです。この上図の三角形より AD の辺の長さを求めます。 高校数学Ⅰの「三角比」では、正弦定理と余弦定理がメインに出てきますよね。 でも、公式が多くて、全部覚えてたら頭がパンクしてしまいますよね。 三角比を攻略するには、sin cos tan の計算や正 三角比6|正弦定理の使い方を具体例から考えよう 三角比を学ぶことで正弦定理と余弦定理という三角形に関する非常に便利な定理を証明することができます. だということは容易に想像が付きますね( 余弦定理 は次の記事で扱います




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
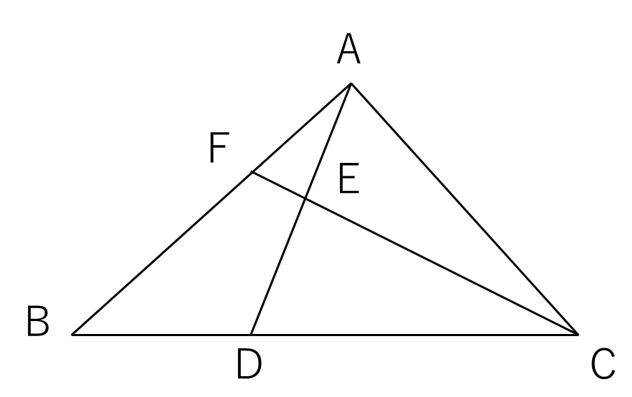
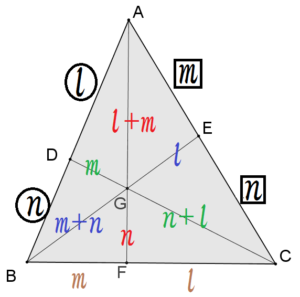
三角形の角の二等分線の性質の証明がわかる5ステップ ゆうき先生 三角形の二等分線の定理の証明は、 補助線をひく 相似な図形をみつける 辺の比に注目する 二等辺三角形をさがす 証明をかく の5ステップだよ。頂角が等しい二つの三角形の面積比 b apq abc = ap×aq ab×ac 8 斜めに置かれた三角形の面積公式 b abc=l×h× 1 2 9 台形上の上底と下底に平行な線分の長さ b pq= × × 10 中線定理 d ab2ac2=2(am2bm2) 11 内接円を利用した三角形の面積 b右の三角形を見てみよう。 点D、E、F は 辺AB を 4等分 するよう においてある。 点G、H、I は 辺AC を 4等分 するよう においてある。



三角形と比の定理 Geogebra



三角形と比
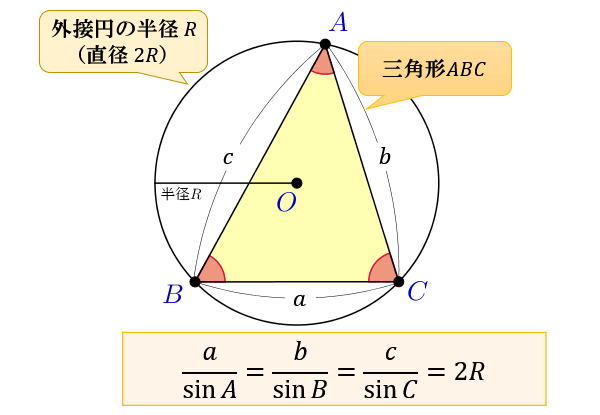
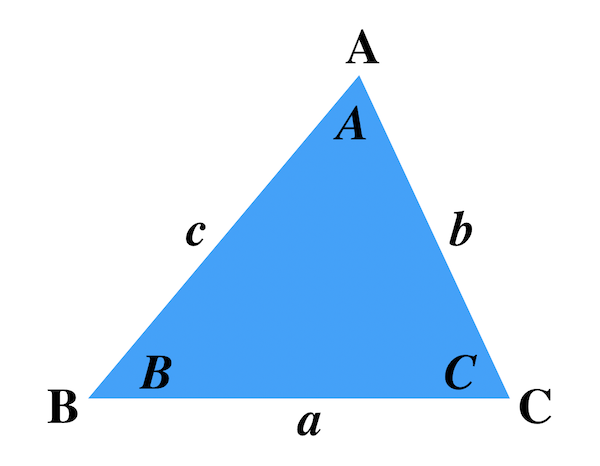
abc が鈍角三角形のときも、同様に証明できます。興味のある人は挑戦してみましょう。 まとめ 正弦定理・余弦定理の内容とそれらを用いた代表的な問題の解き方を説明しました。 正弦定理と余弦定理は、「図形と計量」の分野における基本中の基本です。三角比 三角形の解法 三角形の解法 A B C a c b A, B, C, a, b, c のうち, 3 つがわかる⇒ 他の3 つもわかる。 余弦定理 a2 = b2 c2 −2bc cosA b2 = c2 a2 −2cacosB c2 = a2 b2 −2abcosC 正弦定理 a sinA b sinB c sinC = 2R (R 外接円の半径) 内角の和 AB C = 180 小山哲也 電気リメディアル数学講座第6 回三角形と比の定理 △ABC において、 点D、E をそれぞれ 辺AB、AC 上、また はその延長上の点とするとき次のことがいえる。
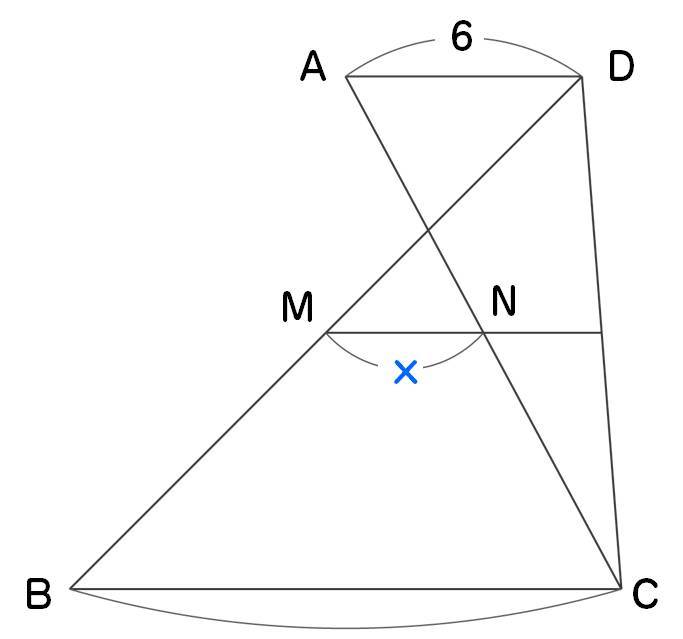



動画で学習 2 三角形と比の定理の逆 数学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
られたときに,三角 形の残りの要素を求 めることができる。 ③正弦定理・余弦定 理を三角形の決定条 件と関連付けて理解 している。 三 角 形 の 面 積 ④三角形の面積を三 角比を活用して求め ようとしている。 ④三角形の面積と辺 の長さの関係から内




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
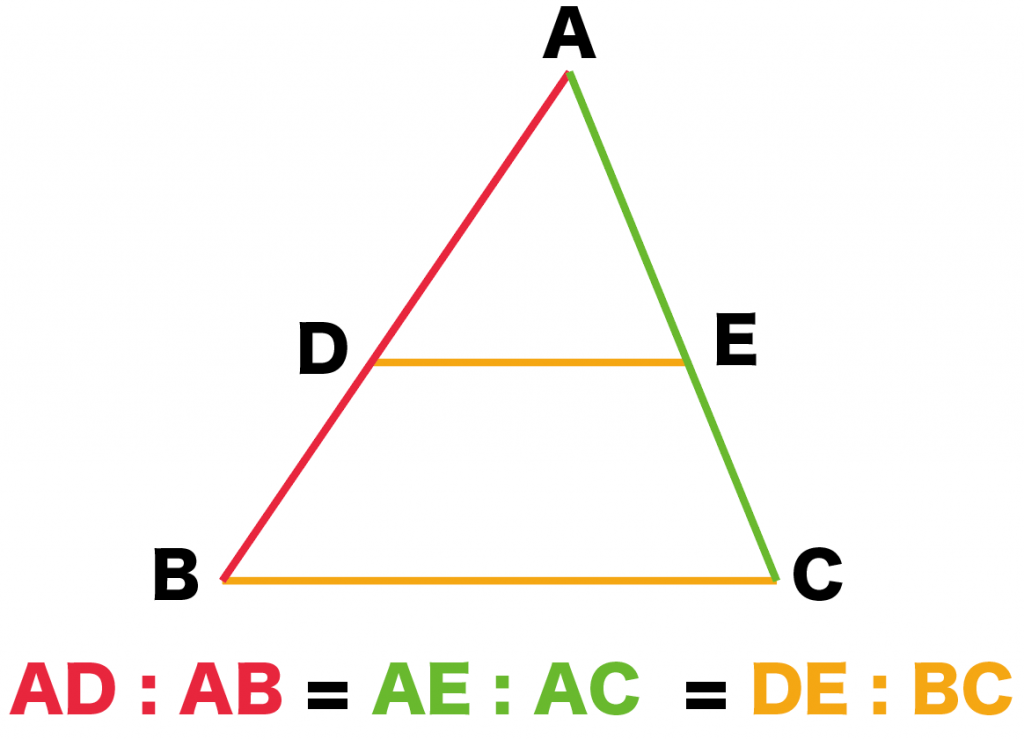



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
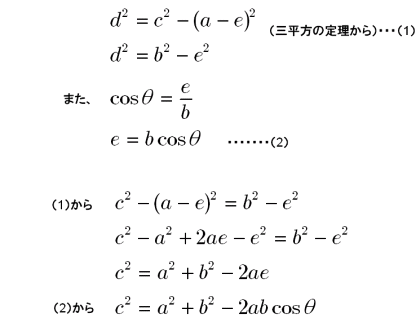



三角比 余弦定理 大人が学び直す数学




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




平面図形をマスター 三角形の面積比 応用編その3




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中学数学3 平行線と線分の比の証明 中学数学 By となりがトトロ マナペディア




Tossランド 三角比の公式 の暗記プリント Dl可




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




この三角形と比の定理というのは Adcと Edbが相似であるから使えるものですか Clear
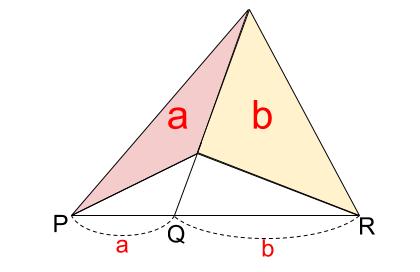



メネラウスの定理 最終奥義 高校数学の無料オンライン学習サイトko Su



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



1
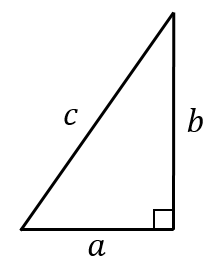



直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学



三角形と比の定理の逆の証明です Df Acとなるように補助線 Yahoo 知恵袋
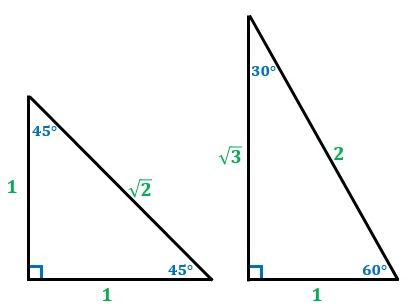



直角三角形の辺の比 東久留米 学習塾 塾長ブログ
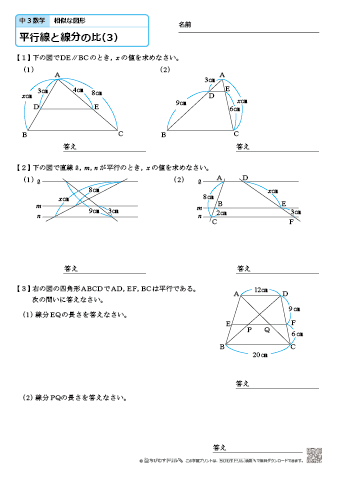



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



三平方の定理から円周率を計算してみる Yamav1 02bのブログ




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



M 2 三角形の辺の比を求める 2 Solid Line
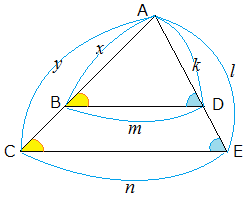



平行線と線分の比
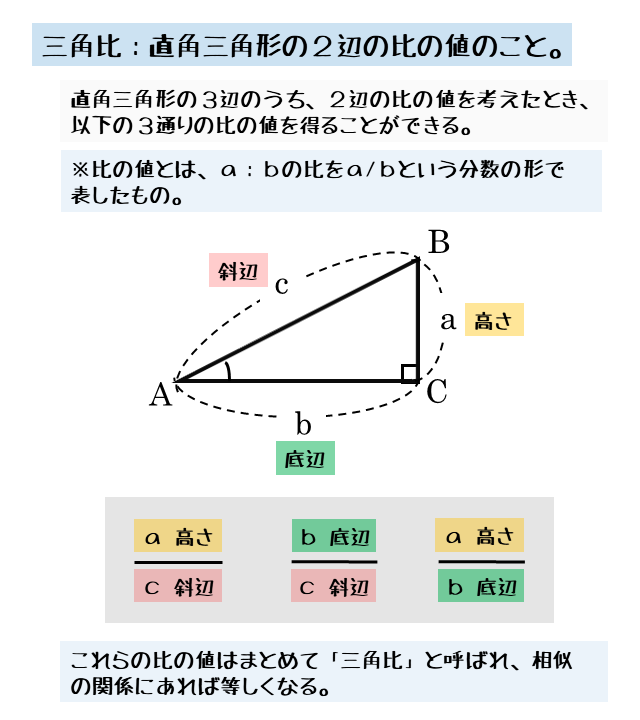



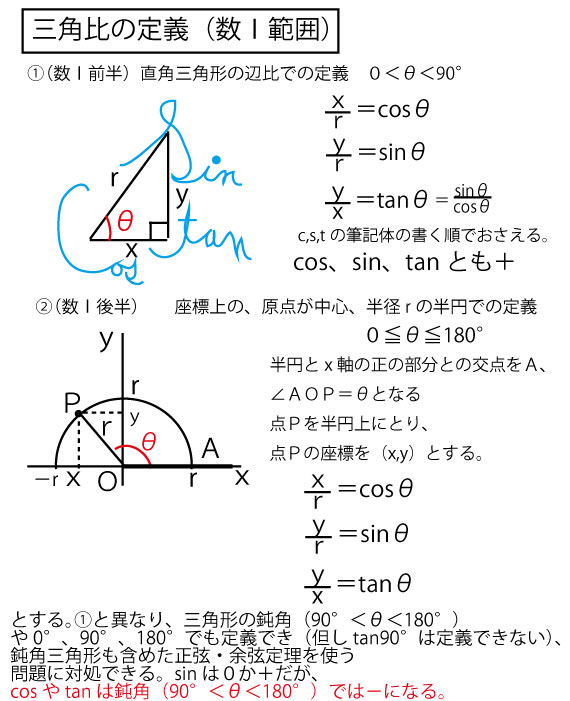
図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平行線と線分の比の定理 の問題の解き方 数学fun
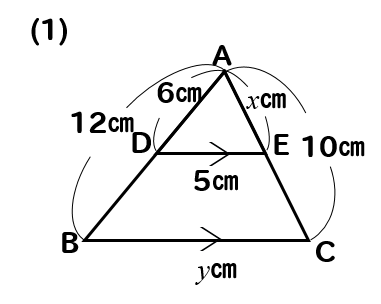



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
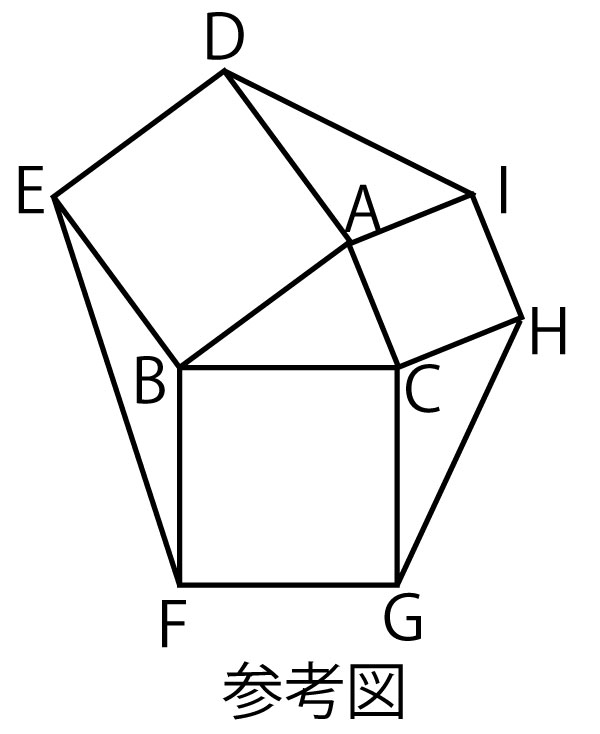



21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




平面図形をマスター 三角形の面積比 応用編その3



1
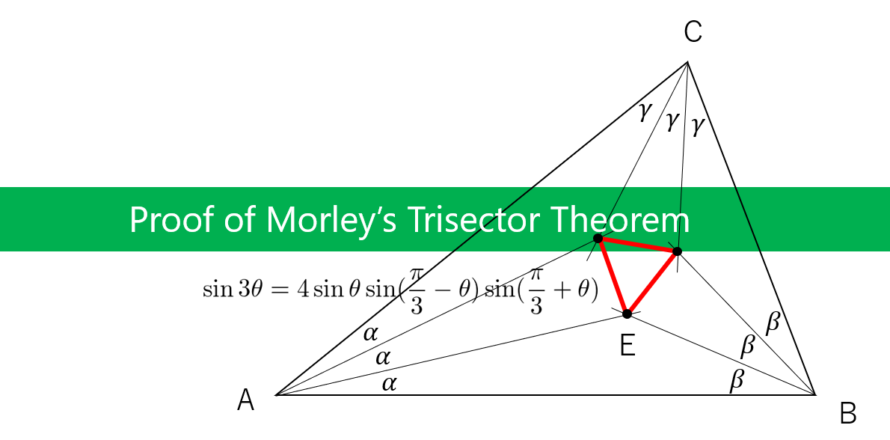



モーリーの定理の証明 三角比を使った方法 数学 統計教室の和から株式会社




苦手を克服 数学aの平面図形で使う定理の一覧 数学a By となりがトトロ マナペディア
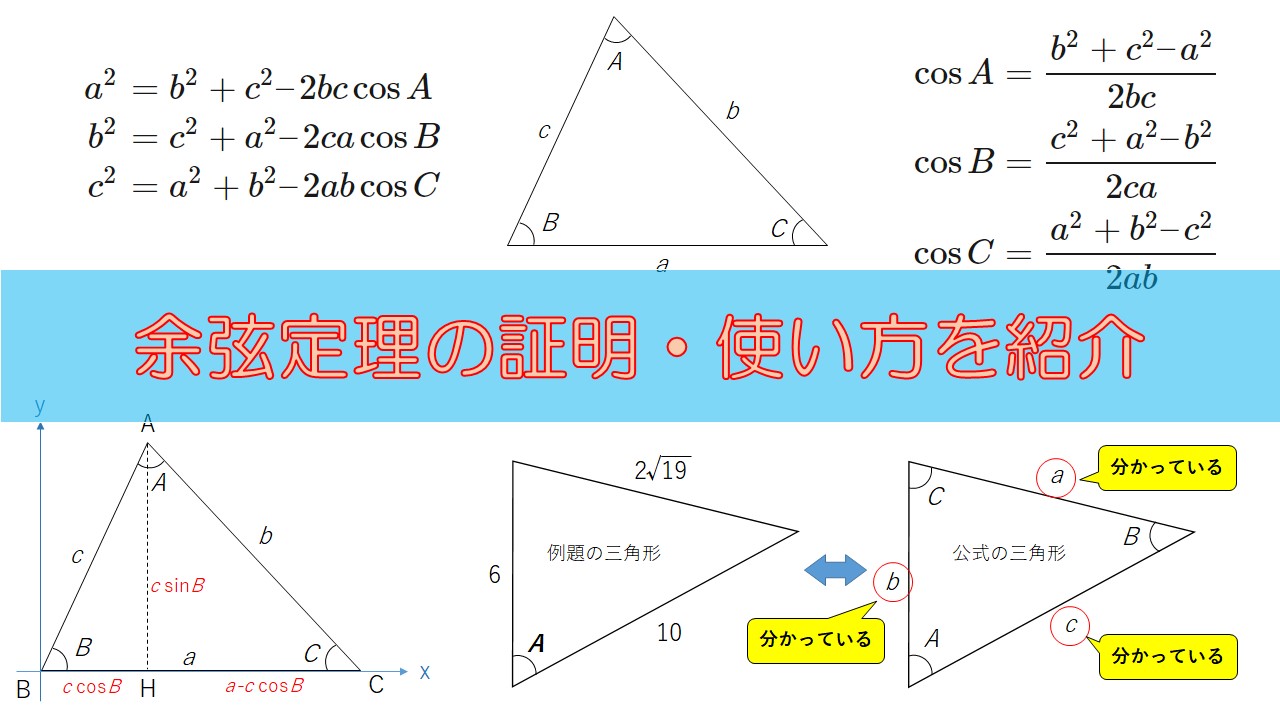



高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト




三角比 高校物理の備忘録
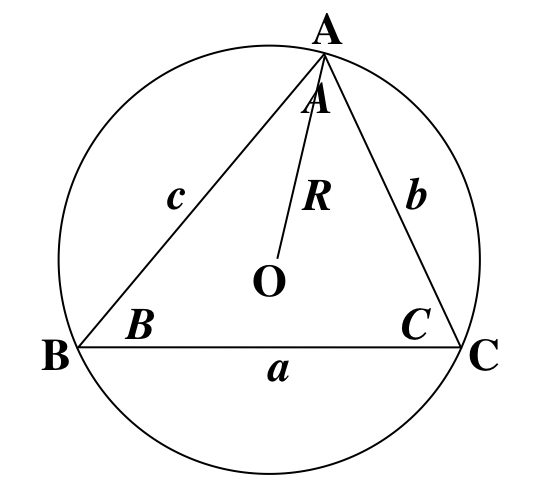



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局
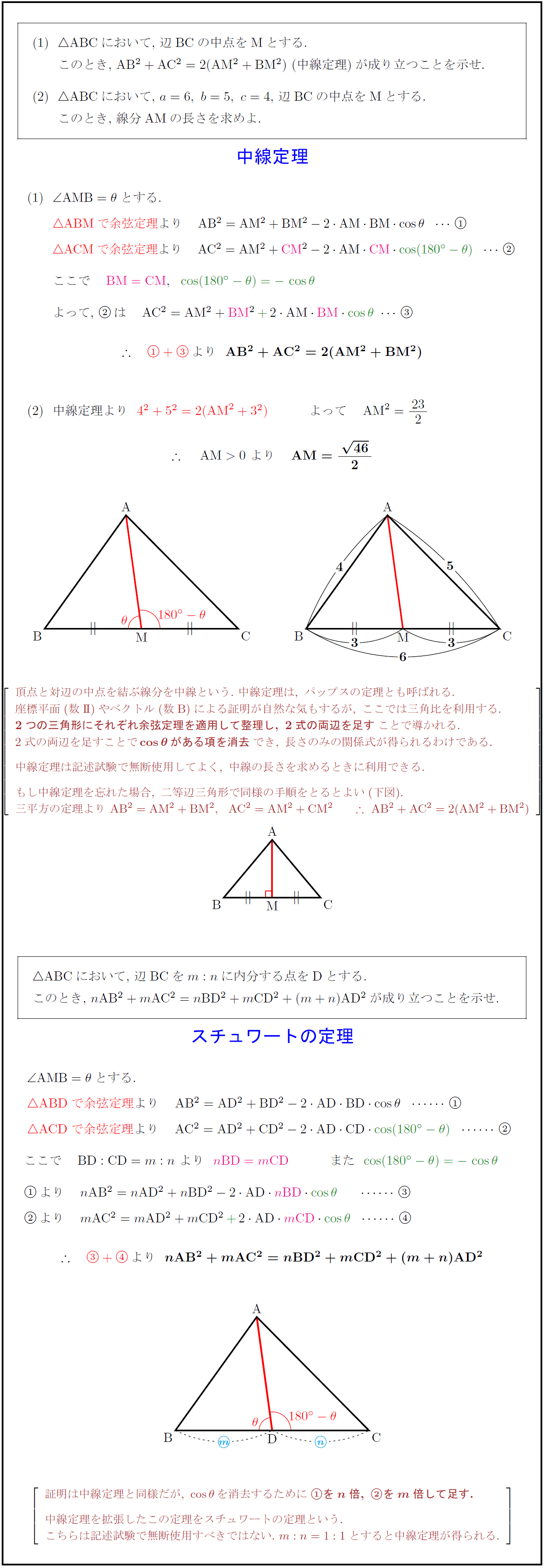



高校数学 中線定理 パップスの定理 とスチュワートの定理の三角比による証明 受験の月




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



三角形と比



1




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題




中3 三角形と比の定理の逆 中学生 数学のノート Clear




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学 図形の相似




平面図形をマスター 三角形の面積比 応用編その3




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




数学 中3 51 平行線と線分の比 中点連結定理編 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



1



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




黄金三角形による18 シリーズの三角比 おいしい数学




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




平面図形をマスター 三角形の面積比 応用編その3




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




数学 中3 49 平行線と線分の比 基本編 Youtube




三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



対線比の定理 Fukusukeの数学めも




余弦定理 は三平方の定理の進化版 余弦定理は2つある




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




わかりやすい三角比と基本公式 Irohabook




三角形と比の定理の証明3 Geogebra
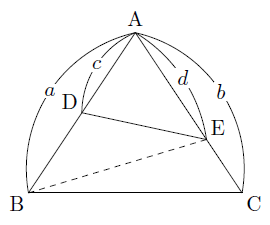



1角共有の三角形の面積比 まなびの学園
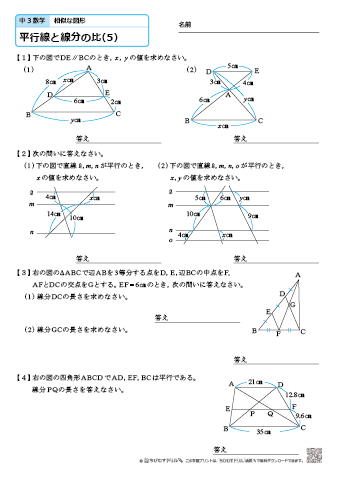



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
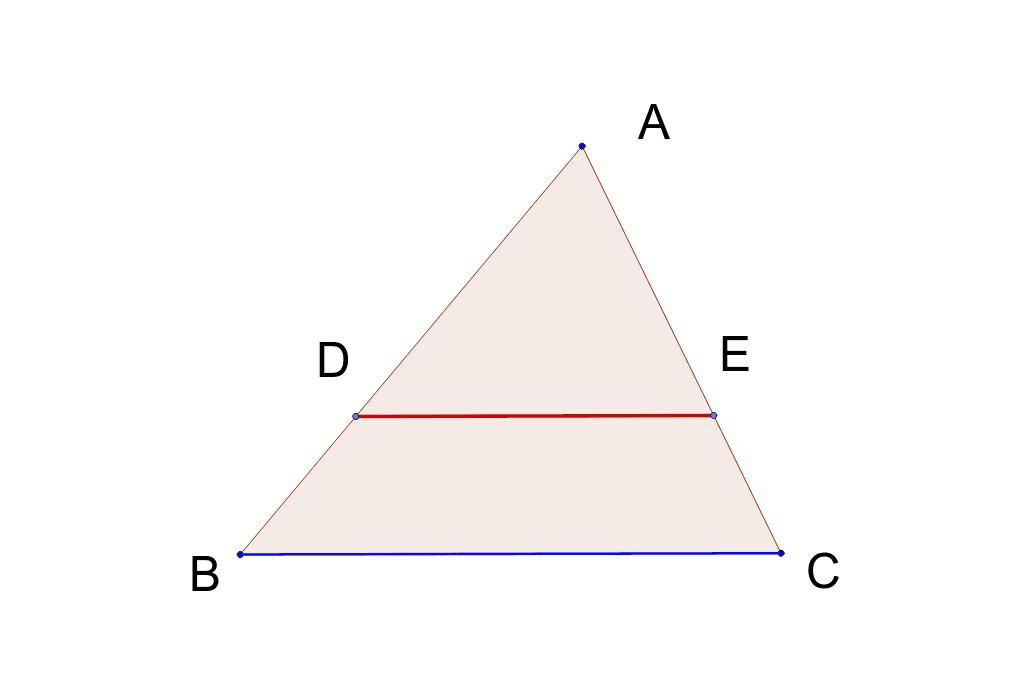



三角形と比の定理の逆 Geogebra




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
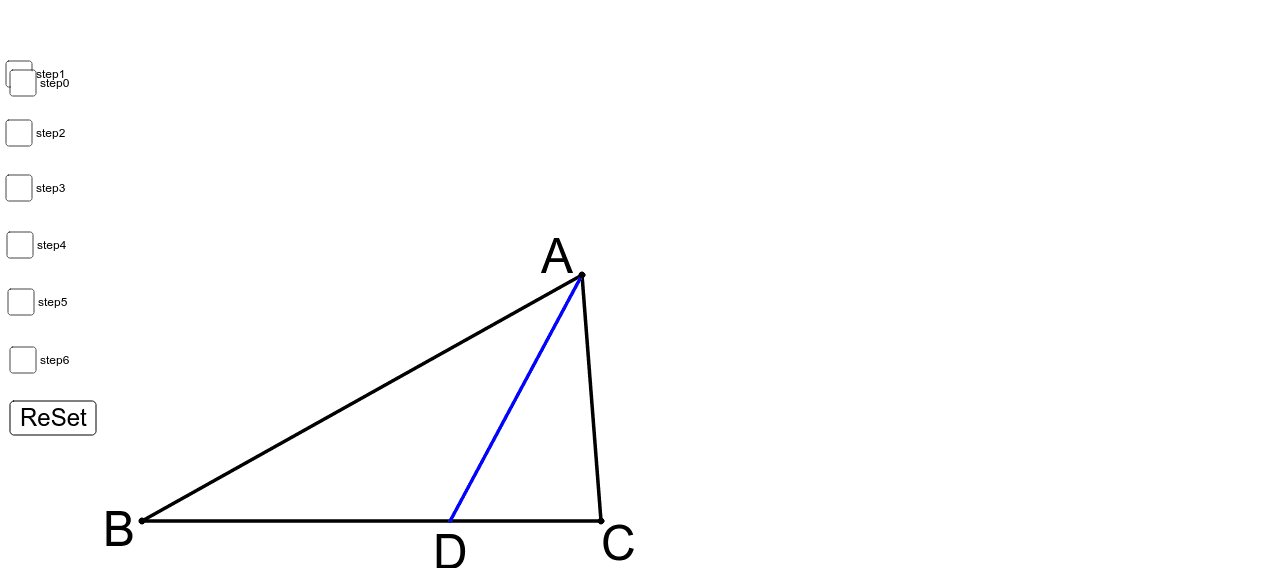



三角形と比の定理の証明1 Geogebra




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




高校数学 三角比 使って覚える三角比の基本公式 数学の面白いこと 役に立つことをまとめたサイト




5分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ




15 シリーズの三角比 おいしい数学




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角比の測量への利用 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




三角形の面積比 数学の偏差値を上げて合格を目指す
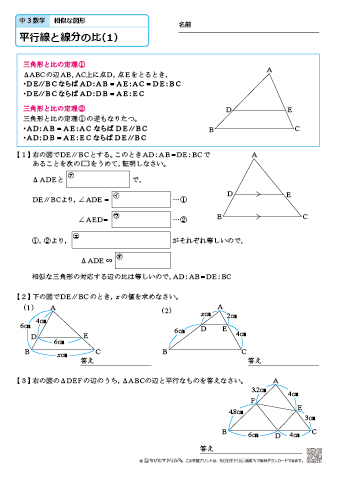



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似



三角比は直角三角形が基本 理系男子の独り善がり




数学 中3 61 三平方の定理 基本編 Youtube



21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中点連結定理と相似 定理の逆や平行四辺形の証明 応用問題の解き方 リョースケ大学




余弦定理で角度を求める方法 数学の星



0 件のコメント:
コメントを投稿